Binary options are popular among beginner traders because they are very easy to understand. A binary option allows the trader to bet on whether the price of an asset will be above or below a certain target price (usually the current market price) at a future time. If a trader expects the price of an asset to increase, then they would buy a binary call option, which would result in a gain if the price of the asset rises above the target price. On the other hand, if the trader expects the price of the asset to drop, then they would buy a binary put option, which pays off if the price of the asset falls below the target price. The payout from a binary option is either a fixed amount in case the prediction by the trader is correct or nothing at all if the prediction is wrong. As such, these options are also referred to as cash-or-nothing options.
Asymmetric Payout of Binary Options
The reason why binary options are popular is because the payout typically ranges between 70% to 90% over a range of few minutes or hours, which makes them very enticing for a trader who wants to earn quick profits. However, binary options have a negative expected return because the payout is asymmetric. This asymmetry puts the trader at a disadvantage.
To illustrate this point, consider a trader who expects the EURUSD exchange rate to rise over the next hour. The trader decides to buy a binary call option for a cost of $100 and is guaranteed an 80% payout if their prediction is correct regarding the EURUSD rate, but loses everything if the prediction is wrong. If the target (strike) EURUSD price of the binary call option is 1.15 then the payout from the option for different ending price scenarios can be illustrated as per the chart below.
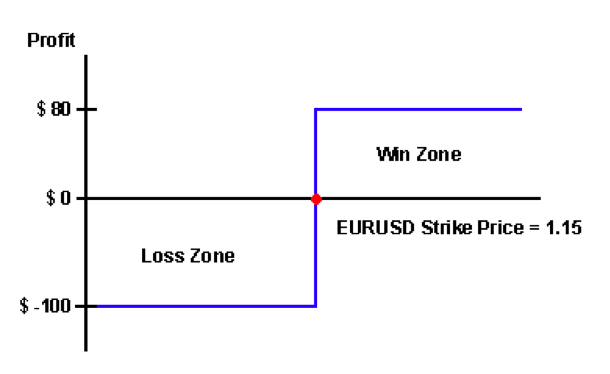
If we assume that the price of the EURUSD exchange rate has an equal probability of rising or falling, then the expected return can be calculated as follows:
Win = $100 x 80% = $80
Lose = -$100 * 100% = -$100
Expected Return = (Win x 50%) + (Lose x 50%) = -$10
In other words, a trader is expected to lose an average of $10 on each bet that is made.
For this game to be fair, the outcome of a win scenario should be equal to the outcome of a lose scenario, which means that a trader needs to be able to win at least 56% of the time to make the expected outcome equal to zero (i.e. $80 x 56% -$100 x 44% = 0).
 The Financial
The Financial